Anomalous Diffraction Theory

Anomalous Diffraction Theory (van de Hulst approximation, eikonal approximation, high energy approximation, soft particle approximation) - approximation developed by van de Hulst describing light scattering for optically soft spheres.

Anomalous diffractions approximation for extinction efficiency is valid for optically soft particles and large size parameter

,

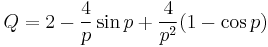where Q is the efficiency factor of scattering, which is defined as the ratio of the scattering cross section and geometrical cross section πa²;
p = 4πa(n – 1)/λ has a physical meaning of the phase delay of the wave passed through the centre of the sphere;
a is the sphere radius, n is the ratio of refractive indices inside and outside of the sphere, and λ the wavelength of the light.
This set of equations was first described by Dutch astronomer van de Hulst. There are extensions to more complicated geometries of scattering target.

Anomalous diffraction approximation offers very approximate but computationally fast technique to calculate light scattering by particles. Absolute value of refractive index has to be close to 1, and size parameter should be large. However, semi-empirical extensions to small size parameter, and larger refractive index are possible. The main advantage of the ADT is that one can (a) calculate, in closed form, extinction, scattering, and absorption efficiencies for many typical size distributions; (b) find solution to the inverse problem of predicting size distribution from light scattering experiments (several wavelengths); (c) for parameterization purposes of single scattering (inherent) optical properties in radiative transfer codes.

^[1]

Another limiting approximation for optically soft particles is Rayleigh scattering which is valid for small size parameter.

Notes and references